Kernel-based clustering algorithms achieve better performance on real world data than Euclidean distance-based clustering algorithms. However, kernel-based algorithms pose two important challenges:
- they do not scale sufficiently in terms of run-time and memory complexity, i.e. their complexity is
quadratic in the number of data instances, rendering them inefficient for large data sets containing millions of data points, and
- the choice of the kernel function is very critical to the performance of the algorithm.
In this project, we aim at developing efficient schemes to reduce the running time complexity and memory requirements of these clustering algorithms and learn appropriate kernel functions from the data.
Approximate Kernel Clustering
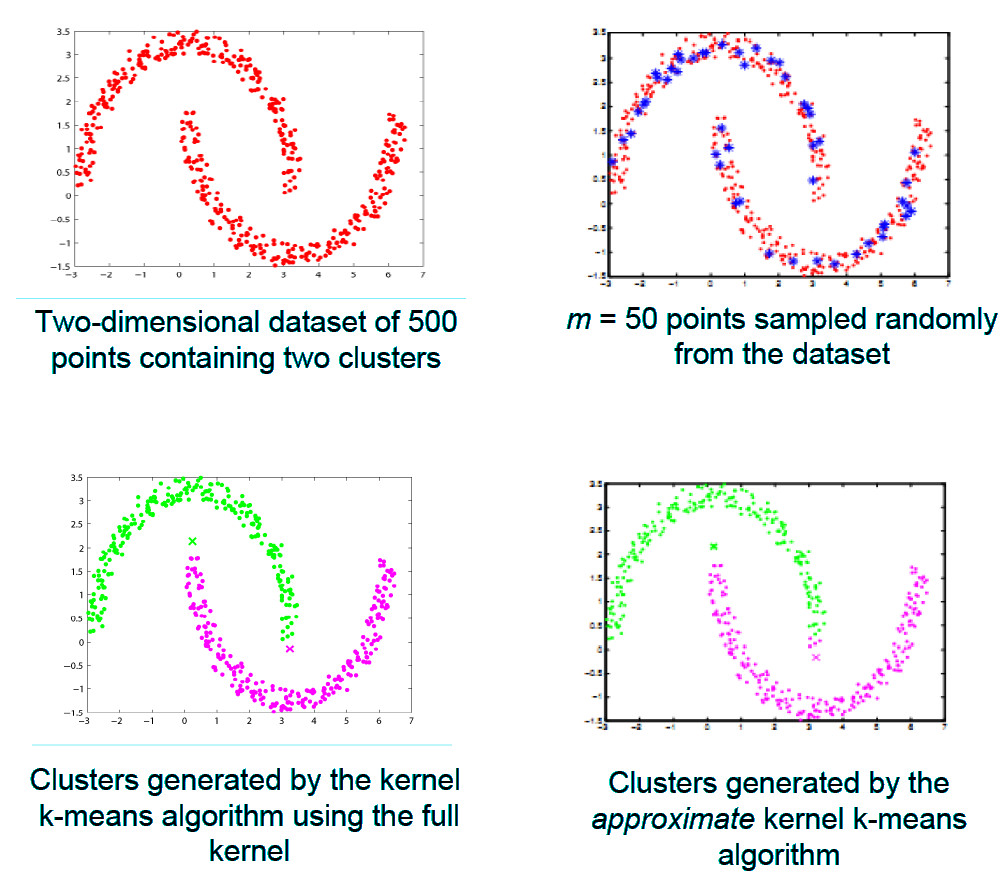
In [1] and [2], we focus on reducing the complexity of the kernel k-means algorithm. The kernel k-means algorithm has quadratic runtime and memory complexity
and cannot cluster more than a few thousands of points efficiently. In [1], we developed an algorithm called Approximate Kernel k-means
which replaces the kernel similarity matrix in kernel k-means with a low rank approximate matrix,
obtained by randomly sampling a small subset of the data set. The approximate kernel matrix is used to obtain the cluster labels for the data
in an iterative manner (see Figure 1). The running time complexity of the approximate kernel k-means algorithm is linear in
the number of points in the data set, thereby reducing the time for clustering by orders of magnitude (compared to the kernel k-means algorithm).
For instance, the approximate kernel k-means algorithm is able to cluster 80 million images from the Tiny data set in about 8 hours on a single core, whereas
kernel k-means requires several weeks to cluster them. The clustering accuracy of the approximate kernel k-means algorithm is close to that of the kernel k-means
algorithm, and the difference in accuracy reduces linearly with the increase in the number of samples.
The approximate kernel k-means algorithm can also be easily parallelized to further reduce the time for clustering.
In [2], random projection is employed to project the data in the kernel space to a low-dimensional space, where the clustering can be performed using
the k-means algorithm. Figure 2 shows some sample clusters
from the Tiny data set obtained using these approximate algorithms.
 |
 |
| Figure. 1 Approximate Kernel k-means |
Figure. 2 Sample clusters from the Tiny data set obtained using the approximate kernel clustering algorithms |
Stream Kernel Clustering
Stream data is generated continuously and is unbounded in size. Stream data clustering, particularly kernel-based clustering, is additionally challenging
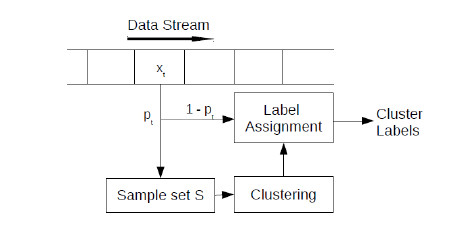
because it is not possible to store all the data and compute the kernel similarity matrix. In [5], we devise a sampling based algorithm which selects a subset
of the stream data to construct an approximate kernel matrix. Each data point is sampled as it arrives, with probability proportional to its importance
in the construction of the low-rank kernel matrix. Clustering is performed in linear time using k-means, in a low-dimensional space
spanned by the eigenvectors corresponding to the top eigenvalues of the kernel matrix constructed from the sampled points. Points which are not sampled are
assigned labels in real-time by selecting the cluster center closest to them (Figure 3).
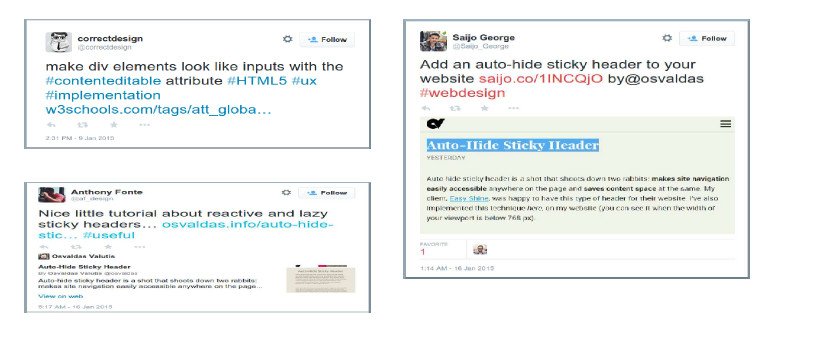
We evaluated this algorithm on the Twitter stream, which was clustered with high accuracy at a speed of about 1 Mbps. Figure 4 shows sample tweets from the
cluster representing the #HTML hashtag.
 |
 |
| Figure. 3 Approximate Stream kernel k-means |
Figure. 4 Cluster representing #HTML from the Twitter stream |
Relevant Publication(s)
[1] R. Chitta, R. Jin, T. C. Havens, and A. K. Jain, "Approximate Kernel k-means: solution to Large Scale Kernel Clustering", KDD, San Diego, CA, August 21-24, 2011.
[2] T. C. Havens, R. Chitta, A. K. Jain, and R. Jin, "Speedup of Fuzzy and Possibilistic Kernel c-Means for Large-Scale Clustering", Proc. IEEE Int. Conf. Fuzzy Systems, Taipei, Taiwan, June 27-30, 2011.
[3] R. Chitta, R. Jin, and A. K. Jain, "Efficient Kernel Clustering using Random Fourier Features", ICDM, Brussels, Belgium, Dec. 10-13, 2012.
[4] R. Chitta, R. Jin, and A. K. Jain, "Scalable Kernel Clustering: Approximate Kernel k-means", arXiv preprint arXiv:1402.3849, 2014.
[5] R. Chitta, R. Jin, and A. K. Jain, "Stream Clustering: Efficient Kernel-Based Approximation using Importance Sampling", (Under Review).



