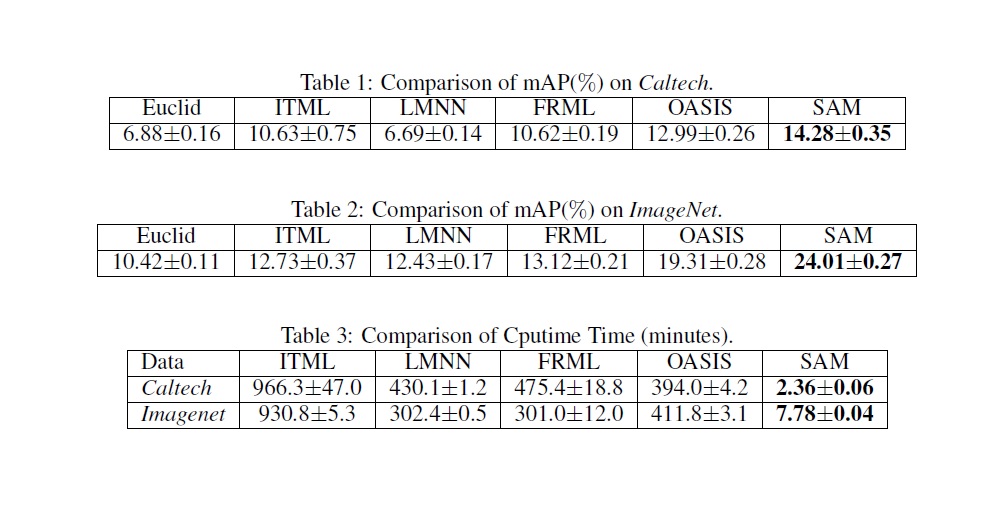
A fundamental problem in machine learning is to assess the similarity or dissimilarity between objects, patterns, and data points. Distance metric learning addresses this fundamental issue by learning a distance metric from a set of training examples such that “similar” instances are close to each other while “dissimilar” instances are separated by a large distance. Distance metric learning has been applied to many tasks in computer vision, face detection and recognition, object tracking and video event detection. Nowadays high dimensional data appears in almost every application domain of machine learning. In order to capture diverse pattern in the visual content of images and temporal correlation among video frames, hundreds of thousands of features are extracted, leading to very high dimensional vector representations. Besides high dimensionality, the amount of data available for learning and mining has grown exponentially in recent years. The computational challenge of high dimensional DML arises from the fact that the number of parameters to be estimated increases quadratically in the number of dimensions. The computational challenge is further complicated by the constraint that the learned distance metric has to be a Positive Semi-Definite (PSD) matrix. To ensure a learned distance metric M to be PSD, we need to perform the eigenvalue decomposition of M, an expensive operation whose cost is cubic in the dimensionality. Another concern with high dimensional DML is the overfitting problem. Again, this is because the number of independent variables in distance metric grows quadratically in dimensionality. This project aims to develop efficient learning algorithms to explicitly address the computational challenges in large-scale high dimensional DML. Analysis for better understanding the generalization properties of regularized empirical minimization for high dimensional DML is also developed. In one of the studies conducted in this project, we developed a similarity learning algorithm [1]. We formulated the similarity learning as a matrix regression problem. High dimensionality problem is addressed by taking low rank assumption and solving partial matrix by alternating method. The large scale problem is tried to be solved my utilizing random projections. In the table, comparisons of mean average precisions and computational times for different metric learning methods and the method developed in our study which is denoted as SAM are given.
 |
Relevant Publication(s)
1. Q. Qian, J. Hu, R. Jin, J. Pei and S. Zhu, “Distance Metric Learning Using Dropout: A Structured Regularization Approach”, Proceedings of 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD'14), 2014.
 |

